Mean, median, and mode are fundamental concepts in statistics that help us make sense of data. These measures of central tendency provide insights into the distribution and behavior of numerical data, making them essential for data analysis. By understanding the connections between mean, median, and mode, we can better interpret datasets and make informed decisions.
Whether you're a student learning statistics for the first time or a professional working with large datasets, mastering these concepts is crucial. This article delves into the intricacies of mean, median, and mode, exploring their definitions, applications, and interconnections. By the end of this guide, you'll have a solid grasp of how these statistical measures work together to paint a complete picture of data.
This guide is designed to be accessible to everyone, regardless of their statistical background. We'll cover everything from basic definitions to advanced applications, ensuring that you leave with a comprehensive understanding of mean median mode connections.
Read also:Unveiling The Remarkable Life And Achievements Of Spencer Jones
Table of Contents
Introduction to Mean Median Mode
Definitions of Mean, Median, and Mode
Examples of Mean, Median, and Mode
Differences Between Mean, Median, and Mode
Connections Between Mean Median Mode
Read also:Marty Stuart The Legendary Country Music Icon
Statistical Tests Involving Mean Median Mode
Tools for Calculating Mean Median Mode
Introduction to Mean Median Mode
The foundation of statistical analysis lies in understanding the central tendencies of data, and mean, median, and mode are the pillars of this foundation. These measures provide different perspectives on the same dataset, offering insights into its distribution, symmetry, and overall behavior. Each measure has its strengths and limitations, and their interplay reveals the nuances of the data being analyzed.
In many real-world scenarios, datasets are complex and require a multifaceted approach to interpretation. By examining the relationships between mean, median, and mode, analysts can uncover patterns and trends that might otherwise go unnoticed. This section will explore the importance of these measures and how they contribute to a deeper understanding of data.
For instance, in business analytics, understanding the connections between mean median mode can help companies make strategic decisions. Similarly, in scientific research, these measures are indispensable for drawing accurate conclusions from experimental data. As we move forward, we'll delve deeper into each concept and how they relate to one another.
Definitions of Mean, Median, and Mode
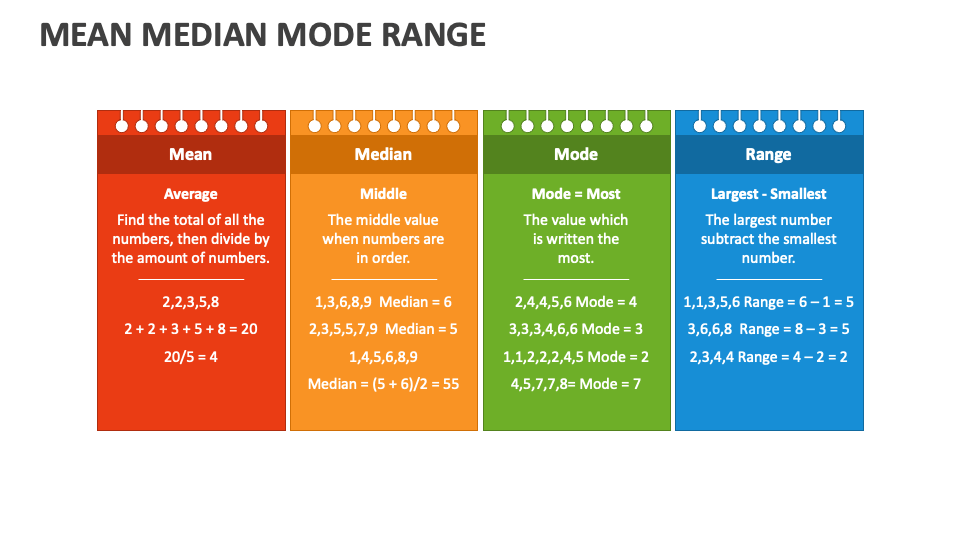
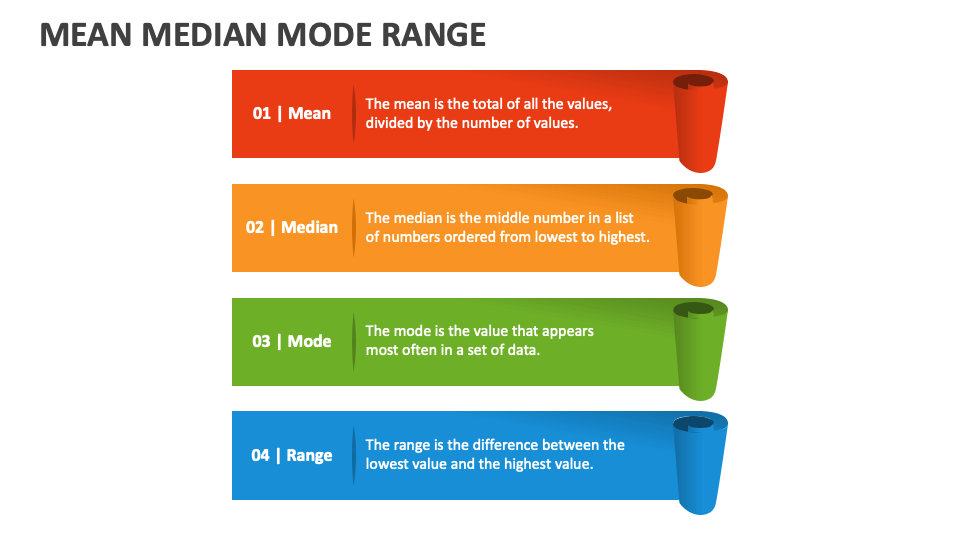
What is Mean?
The mean, often referred to as the average, is calculated by summing all the values in a dataset and dividing by the total number of values. It is the most commonly used measure of central tendency due to its simplicity and wide applicability. However, the mean can be influenced by outliers, which may skew the results if not handled carefully.
What is Median?
The median represents the middle value in a dataset when the numbers are arranged in ascending or descending order. Unlike the mean, the median is less affected by extreme values or outliers, making it a more robust measure in certain situations. For datasets with an odd number of values, the median is the central number, while for even-numbered datasets, it is the average of the two middle numbers.
What is Mode?
The mode is the value that appears most frequently in a dataset. Unlike the mean and median, the mode can be used for both numerical and categorical data. A dataset can have one mode (unimodal), multiple modes (multimodal), or no mode at all if all values occur with equal frequency.
Examples of Mean, Median, and Mode
To better understand these concepts, let's consider a sample dataset: 5, 7, 9, 12, 15.
- Mean: (5 + 7 + 9 + 12 + 15) / 5 = 9.6
- Median: The middle value is 9.
- Mode: There is no mode since all values occur only once.
Now, let's examine a dataset with repeated values: 3, 5, 5, 7, 9.
- Mean: (3 + 5 + 5 + 7 + 9) / 5 = 5.8
- Median: The middle value is 5.
- Mode: The mode is 5, as it occurs twice.
Differences Between Mean, Median, and Mode
While mean, median, and mode are all measures of central tendency, they differ in their calculation methods and applications. The mean is influenced by all values in the dataset, making it sensitive to outliers. The median, on the other hand, is resistant to extreme values and provides a more stable measure in skewed distributions. The mode is unique in that it can be applied to both numerical and categorical data, offering insights into the most frequent occurrences.
Choosing the right measure depends on the nature of the data and the specific question being addressed. For example, in income analysis, the median is often preferred over the mean because it provides a more accurate representation of the typical income level in the presence of a few high earners.
Connections Between Mean Median Mode
Relationship in Symmetrical Distributions
In a perfectly symmetrical distribution, such as the normal distribution, the mean, median, and mode coincide at the center of the distribution. This alignment makes it easier to interpret the data and draw conclusions about its central tendency.
Relationship in Skewed Distributions
In skewed distributions, the mean, median, and mode diverge, with the mean being pulled in the direction of the skew. For positively skewed data, the mean is greater than the median, while for negatively skewed data, the mean is less than the median. The mode remains unaffected by skewness, providing a stable reference point.
Applications in Real Life
Business Analytics
In business, mean median mode connections are used to analyze sales data, customer demographics, and market trends. For example, a retailer might use the median income of its target audience to determine pricing strategies, while the mode could reveal the most popular product category.
Healthcare
In healthcare, these measures are crucial for understanding patient data, such as average recovery times, median hospital stays, and the most common diagnoses. By analyzing these metrics, healthcare providers can improve patient outcomes and allocate resources more effectively.
Education
Educators use mean, median, and mode to evaluate student performance and design curricula. For instance, the median score on a standardized test might indicate the typical level of achievement, while the mode could highlight the most common areas of difficulty.
Impact of Skewed Data
Skewed data can significantly affect the interpretation of mean, median, and mode. In positively skewed distributions, the mean is pulled to the right, while in negatively skewed distributions, it is pulled to the left. The median remains a more reliable measure in such cases, as it is less influenced by extreme values. Understanding the impact of skewness is essential for accurate data analysis and decision-making.
Statistical Tests Involving Mean Median Mode
T-Tests
T-tests are commonly used to compare the means of two groups, determining whether the observed differences are statistically significant. These tests assume that the data is normally distributed, highlighting the importance of understanding the relationship between mean, median, and mode in such analyses.
Mann-Whitney U Test
For non-parametric data, the Mann-Whitney U test compares the medians of two groups, offering an alternative to t-tests when the data does not meet normality assumptions. This test underscores the versatility of the median in statistical analysis.
Tools for Calculating Mean Median Mode
Several tools and software programs are available for calculating mean, median, and mode, including Excel, Python, and R. These tools simplify the process of data analysis, allowing users to focus on interpretation and application. For example, Excel provides built-in functions for calculating these measures, while Python's pandas library offers powerful data manipulation capabilities.
Conclusion and Next Steps
In conclusion, mean, median, and mode are essential tools for understanding and interpreting data. Their connections provide valuable insights into the behavior of datasets, enabling more informed decision-making across various fields. By mastering these concepts, you can enhance your analytical skills and contribute meaningfully to data-driven discussions.
We encourage you to explore further by practicing with real datasets and experimenting with different statistical tools. Don't hesitate to leave a comment or share this article with others who might benefit from it. For more in-depth resources, check out our other articles on statistics and data analysis.
References:
- Field, A. (2018). Discovering Statistics Using IBM SPSS Statistics. Sage Publications.
- Gravetter, F. J., & Wallnau, L. B. (2016). Statistics for the Behavioral Sciences. Cengage Learning.